How to Remove Unknown Spouse in Family Tree Maker

Everything you need to know about tree data structures

When you first larn to lawmaking, information technology'south common to acquire arrays as the "main information construction."

Eventually, you will learn about hash tables likewise. If y'all are pursuing a Informatics degree, y'all accept to take a class on data structure. Yous will as well learn nearly linked lists, queues, and stacks. Those data structures are called "linear" data structures because they all accept a logical kickoff and a logical end.

When we start learning near copse and graphs, it can go actually confusing. We don't shop information in a linear fashion. Both data structures store data in a specific way.

This post is to help you meliorate understand the Tree Data Structure and to analyze any confusion you may have well-nigh it.

In this article, nosotros will learn:

What is a tree
Examples of copse
Its terminology and how it works
How to implement tree structures in lawmaking.

Permit's start this learning journey. :)

Definition

When starting out programming, information technology is mutual to empathise better the linear data structures than data structures similar trees and graphs.

Trees are well-known as a non-linear data structure. They don't store data in a linear style. They organize data hierarchically.

Allow'due south swoop into real life examples!

What exercise I hateful when I say in a hierarchical way?

Imagine a family tree with relationships from all generation: grandparents, parents, children, siblings, etc. We unremarkably organize family trees hierarchically.

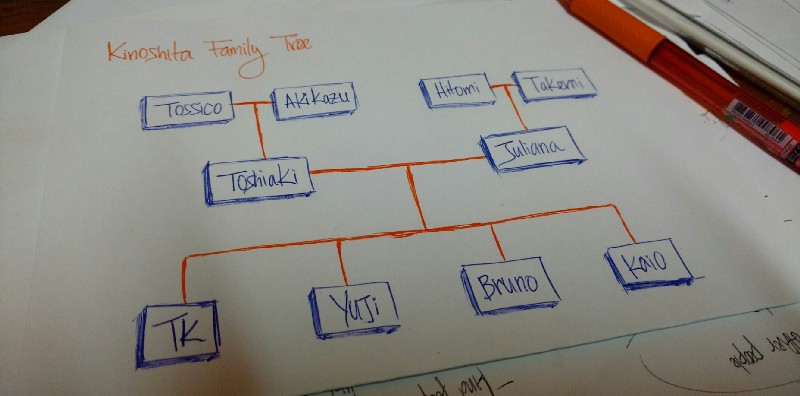
1*MasdC5DmucEU2abIXQe45Q — My family tree

The higher up drawing is is my family tree. Tossico, Akikazu, Hitomi, and Takemi are my grandparents.

Toshiaki and Juliana are my parents.

TK, Yuji, Bruno, and Kaio are the children of my parents (me and my brothers).

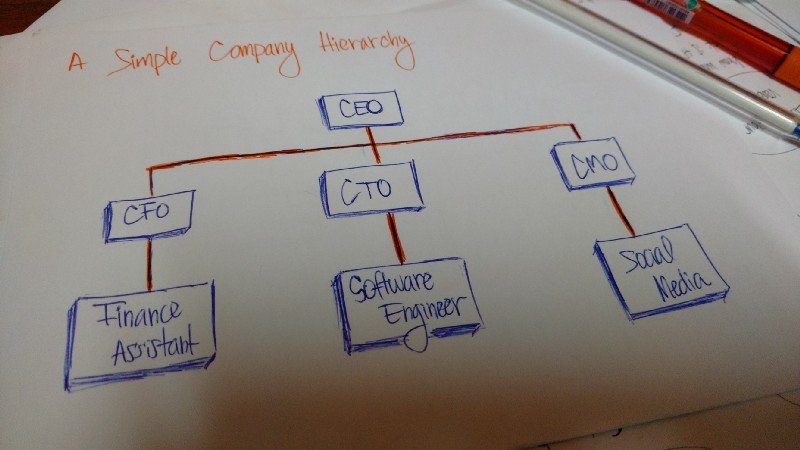
An organization'due south structure is another case of a hierarchy.

1*GsBCmW5E1GuJ3MpH3Zz0Ew — A company'southward structure is an example of a bureaucracy

In HTML, the Document Object Model (DOM) works as a tree.

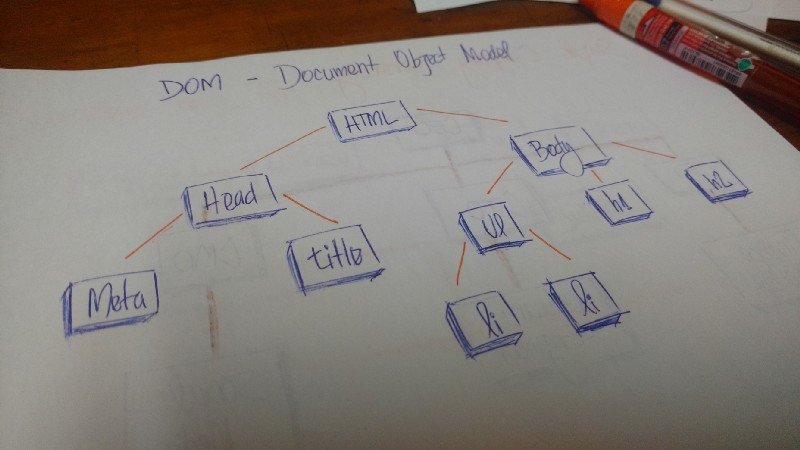
1*dLXUdR4NuIZG8GJdu_Cinw — Document Object Model (DOM)

The HTML tag contains other tags. We have a caput tag and a trunk tag. Those tags contains specific elements. The head tag has meta and title tags. The body tag has elements that bear witness in the user interface, for example, h1, a, li, etc.

A technical definition

A tree is a collection of entities called nodes. Nodes are continued by edges. Each node contains a value or information, and information technology may or may not take a child node .

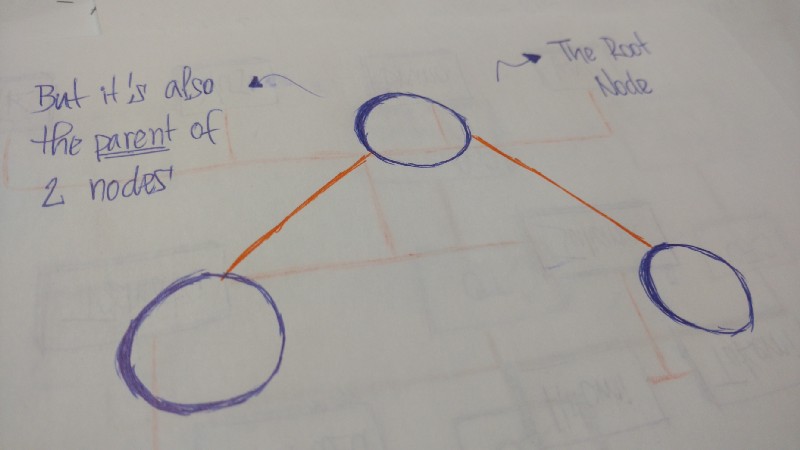
The showtime node of the tree is called the root. If this root node is connected by another node, the root is then a parent node and the connected node is a child.

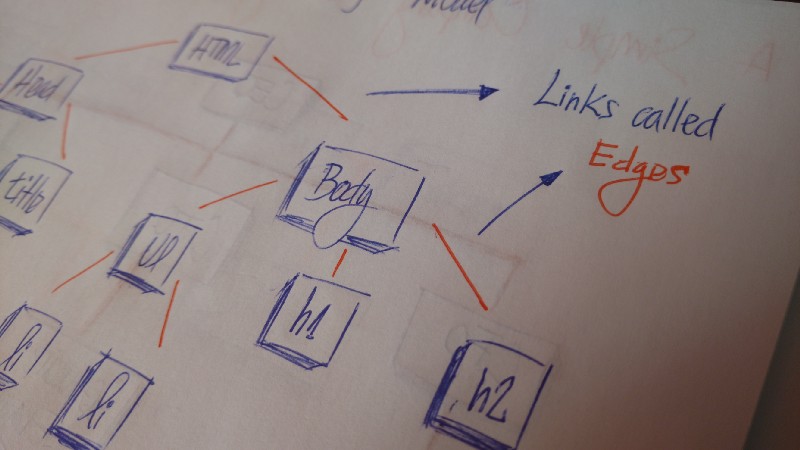
All Tree nodes are connected past links called edges. It's an important role of trees, because information technology's manages the relationship between nodes.

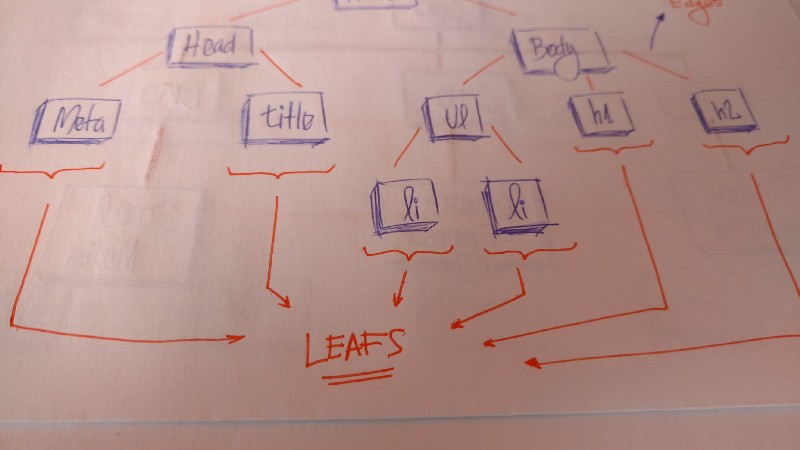
Leaves are the last nodes on a tree. They are nodes without children. Similar real copse, we have the root, branches, and finally the leaves.

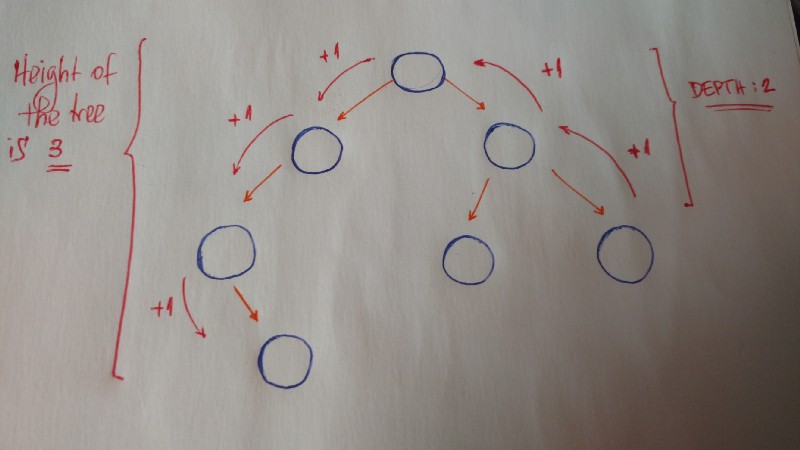
Other of import concepts to understand are meridian and depth.

The acme of a tree is the length of the longest path to a leaf.

The depth of a node is the length of the path to its root.

Terminology summary

Root is the topmost node of the tree
Edge is the link between two nodes
Child is a node that has a parent node
Parent is a node that has an edge to a child node
Leaf is a node that does not have a child node in the tree
Summit is the length of the longest path to a leaf
Depth is the length of the path to its root

Binary trees

Now we will discuss a specific type of tree. We call information technology thebinary tree.

"In reckoner science, a binary tree is a tree data structure in which each node has at the most ii children, which are referred to as the left child and the right kid." — Wikipedia

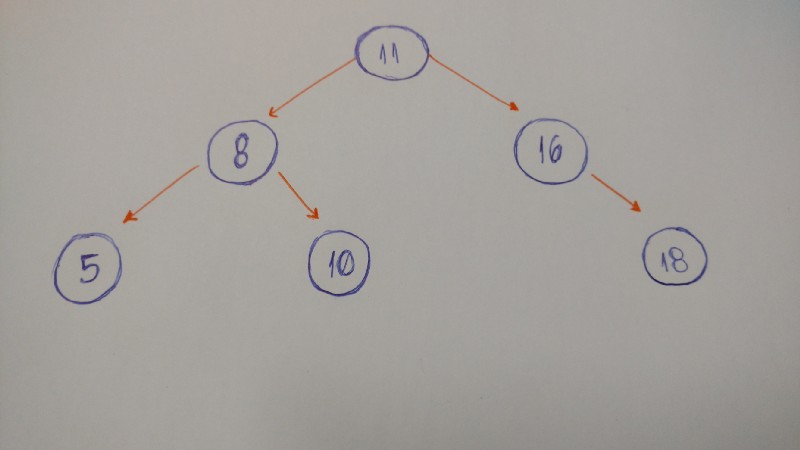
So let's look at an case of a binary tree.

Let's code a binary tree

The kickoff thing we demand to go on in heed when we implement a binary tree is that information technology is a collection of nodes. Each node has three attributes: value, left_child, and right_child.

How practice we implement a simple binary tree that initializes with these iii backdrop?

Allow's take a look.

                class BinaryTree:     def __init__(self, value):         self.value = value         self.left_child = None         self.right_child = None

Here it is. Our binary tree class.

When we instantiate an object, we pass the value (the information of the node) as a parameter. Await at the left_child and the right_child. Both are set to None.

Why?

Considering when we create our node, it doesn't accept whatsoever children. We just have the node information.

Allow'due south test it:

                tree = BinaryTree('a') print(tree.value) # a impress(tree.left_child) # None print(tree.right_child) # None

That'southward it.

We tin can pass the string 'a' as the value to our Binary Tree node. If we print the value, left_child, and right_child, we tin run into the values.

Let's go to the insertion office. What do we demand to do here?

Nosotros will implement a method to insert a new node to the right and to the left.

Here are the rules:

If the current node doesn't have a left child, nosotros just create a new nodeand set it to the current node'due south left_child.
If it does have the left kid, nosotros create a new node and put it in the current left child's place. Classify this left child node to the new node'southward left kid.

Permit's depict it out. :)

Here'due south the code:

                def insert_left(cocky, value):     if self.left_child == None:         self.left_child = BinaryTree(value)     else:         new_node = BinaryTree(value)         new_node.left_child = self.left_child         self.left_child = new_node

Over again, if the current node doesn't take a left child, we merely create a new node and set it to the current node'southward left_child. Or else nosotros create a new node and put it in the current left kid's identify. Classify this left child node to the new node's left kid.

And we do the aforementioned thing to insert a right child node.

                def insert_right(cocky, value):     if cocky.right_child == None:         self.right_child = BinaryTree(value)     else:         new_node = BinaryTree(value)         new_node.right_child = self.right_child         self.right_child = new_node

Washed. :)

Simply not entirely. Nosotros even so need to test it.

Let's build the post-obittree:

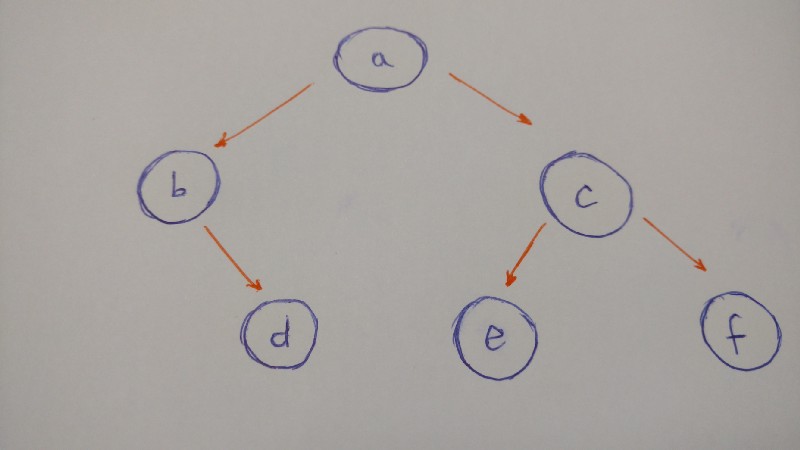
To summarize the analogy of this tree:

a node will be the root of our binary Tree
a left kid is b node
a right kid is c node
b right child is d node (b node doesn't have a left child)
c left child is e node
c correct child is f node
both e and f nodes exercise not have children

So here is the lawmaking for the tree:

                a_node = BinaryTree('a') a_node.insert_left('b') a_node.insert_right('c')  b_node = a_node.left_child b_node.insert_right('d')  c_node = a_node.right_child c_node.insert_left('e') c_node.insert_right('f')  d_node = b_node.right_child e_node = c_node.left_child f_node = c_node.right_child  print(a_node.value) # a print(b_node.value) # b print(c_node.value) # c print(d_node.value) # d print(e_node.value) # east print(f_node.value) # f

Insertion is done.

Now we take to think about tree traversal.

We have two options here: Depth-First Search (DFS) and Breadth-Beginning Search (BFS).

DFS "is an algorithm for traversing or searching tree data structure. One starts at the root and explores as far every bit possible along each branch before backtracking." — Wikipedia
BFS "is an algorithm for traversing or searching tree data structure. It starts at the tree root and explores the neighbor nodes first, before moving to the next level neighbors." — Wikipedia

Then allow's dive into each tree traversal type.

Depth-First Search (DFS)

DFS explores a path all the mode to a foliage before backtracking and exploring another path. Permit'due south take a expect at an instance with this type of traversal.

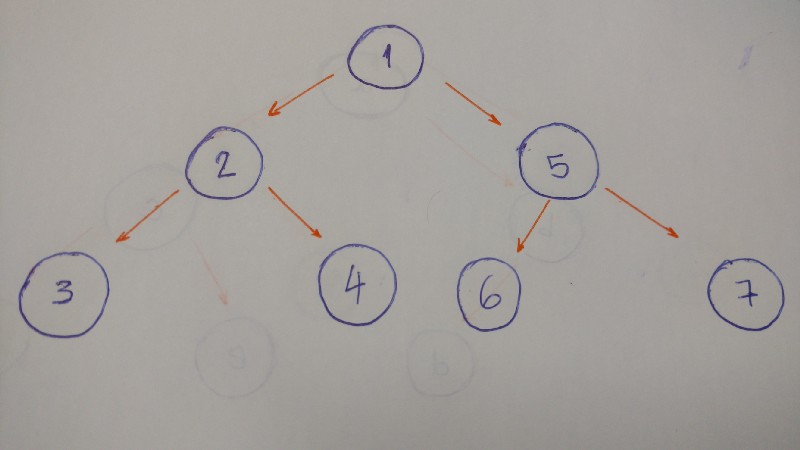
The issue for this algorithm will be one–2–three–four–5–6–seven.

Why?

Permit's pause it down.

Kickoff at the root (1). Print it.

2. Go to the left child (2). Print it.

3. Then go to the left child (three). Impress it. (This node doesn't have whatever children)

4. Backtrack and go the right child (iv). Print it. (This node doesn't have any children)

5. Backtrack to the root node and get to the right child (five). Print it.

half-dozen. Become to the left kid (6). Print it. (This node doesn't have any children)

7. Backtrack and get to the correct child (7). Print it. (This node doesn't take any children)

8. Washed.

When we go deep to the leafage and backtrack, this is called DFS algorithm.

Now that nosotros are familiar with this traversal algorithm, we volition hash out types of DFS: pre-order, in-order, and post-order.

Pre-guild

This is exactly what nosotros did in the in a higher place example.

Impress the value of the node.
Go to the left child and print it. This is if, and but if, it has a left kid.
Go to the right kid and impress it. This is if, and simply if, it has a right child.

                def pre_order(self):     print(self.value)      if self.left_child:         self.left_child.pre_order()      if self.right_child:         self.right_child.pre_order()

In-order

The result of the in-order algorithm for this tree example is 3–ii–4–1–half-dozen–5–7.

The left first, the middle second, and the correct last.

At present allow's code information technology.

                def in_order(self):     if self.left_child:         self.left_child.in_order()      print(self.value)      if self.right_child:         self.right_child.in_order()

Get to the left child and print it. This is if, and merely if, it has a left kid.
Impress the node'south value
Go to the right child and print it. This is if, and only if, it has a right kid.

Post-order

The result of the mail club algorithm for this tree example is iii–4–ii–half dozen–7–v–1.

The left first, the right second, and the middle terminal.

Let's code this.

                def post_order(self):     if cocky.left_child:         self.left_child.post_order()      if cocky.right_child:         self.right_child.post_order()      print(self.value)

Get to the left kid and print information technology. This is if, and only if, information technology has a left child.
Go to the right child and print it. This is if, and only if, information technology has a correct child.
Impress the node's value

Breadth-First Search (BFS)

BFS algorithm traverses the tree level past level and depth past depth.

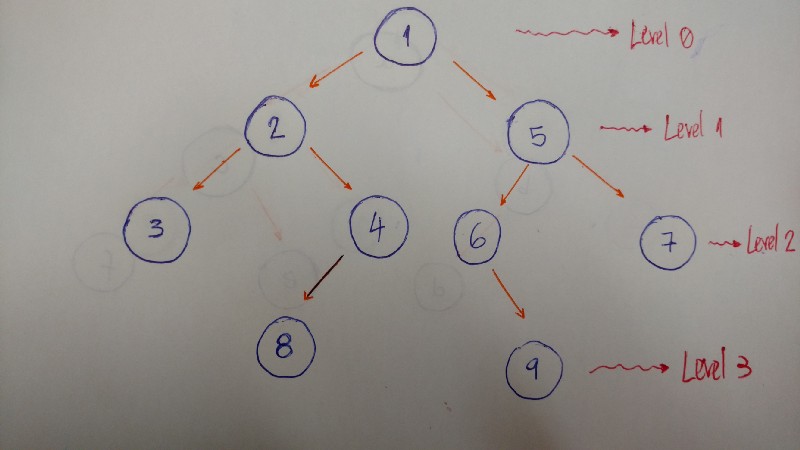
Hither is an example that helps to better explicate this algorithm:

And so we traverse level by level. In this instance, the upshot is ane–ii–5–3–iv–half-dozen–seven.

Level/Depth 0: merely node with value 1
Level/Depth 1: nodes with values 2 and v
Level/Depth 2: nodes with values 3, 4, 6, and 7

Now let's lawmaking it.

                def bfs(self):     queue = Queue()     queue.put(self)      while not queue.empty():         current_node = queue.get()         print(current_node.value)          if current_node.left_child:             queue.put(current_node.left_child)          if current_node.right_child:             queue.put(current_node.right_child)

To implement a BFS algorithm, we use the queue information construction to help.

How does information technology work?

Here's the explanation.

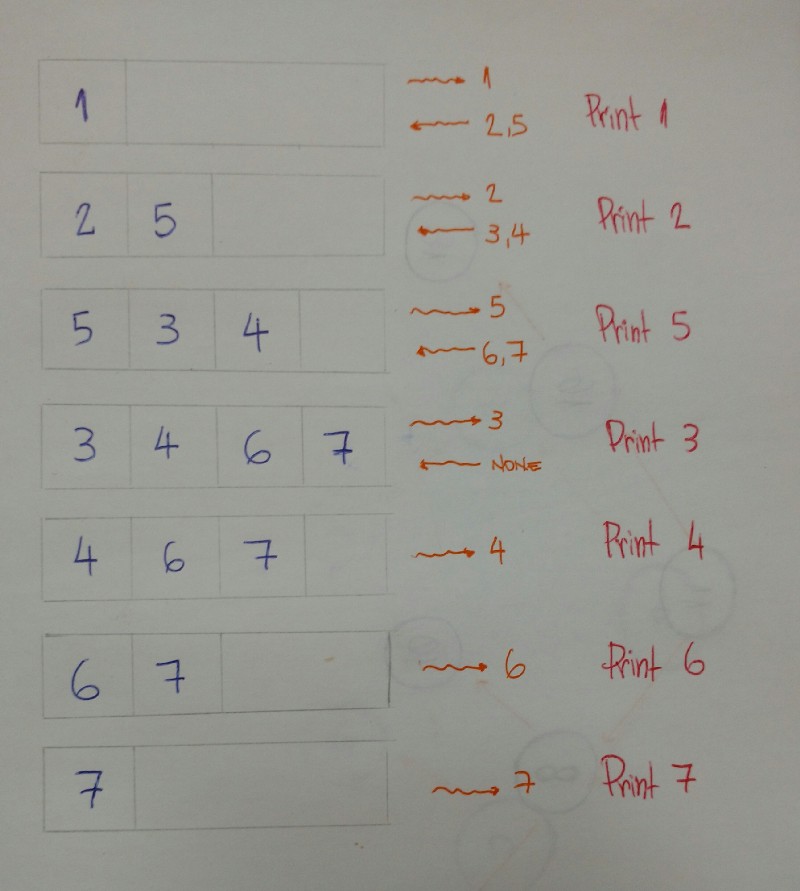
First add together the root node into the queue with the put method.
Iterate while the queue is not empty.
Get the commencement node in the queue, and and then print its value.
Add both left and right children into the queue (if the current nodehas children).
Washed. Nosotros will impress the value of each node, level by level, with our queuehelper.

Binary Search tree

"A Binary Search Tree is sometimes called ordered or sorted binary trees, and information technology keeps its values in sorted guild, so that lookup and other operations tin can utilise the principle of binary search" — Wikipedia

An important belongings of a Binary Search Tree is that the value of a Binary Search Tree nodeis larger than the value of the offspring of its left child, only smaller than the value of the offspring of its right child."

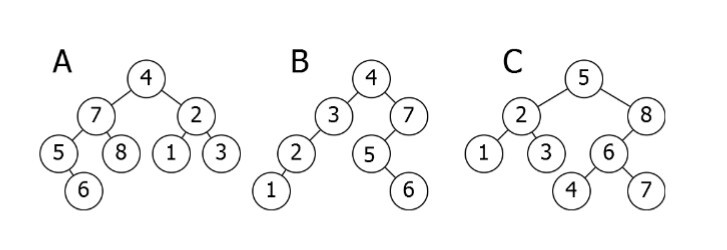
Here is a breakdown of the to a higher place illustration:

A is inverted. The subtree seven–5–8–6 needs to be on the correct side, and the subtree ii–1–3 needs to be on the left.
B is the only correct choice. It satisfies the Binary Search Tree property.
C has one trouble: the node with the value 4. It needs to exist on the left side of the root because it is smaller than 5.

Let's code a Binary Search Tree!

Now information technology's time to lawmaking!

What will we come across here? Nosotros will insert new nodes, search for a value, delete nodes, and the balance of the tree.

Let's beginning.

Insertion: adding new nodes to our tree

Imagine that nosotros have an empty tree and we want to add new nodes with the following values in this order: 50, 76, 21, 4, 32, 100, 64, 52.

The first thing nosotros need to know is if 50 is the root of our tree.

We can now commencement inserting node past node.

76 is greater than 50, so insert 76 on the right side.
21 is smaller than 50, so insert 21 on the left side.
4 is smaller than 50. Node with value 50 has a left kid 21. Since four is smaller than 21, insert it on the left side of this node.
32 is smaller than 50. Node with value 50 has a left child 21. Since 32 is greater than 21, insert 32 on the right side of this node.
100 is greater than 50. Node with value 50 has a correct child 76. Since 100 is greater than 76, insert 100 on the right side of this node.
64 is greater than l. Node with value 50 has a right child 76. Since 64 is smaller than 76, insert 64 on the left side of this node.
52 is greater than 50. Node with value 50 has a right child 76. Since 52 is smaller than 76, node with value 76 has a left child 64. 52 is smaller than 64, so insert 54 on the left side of this node.

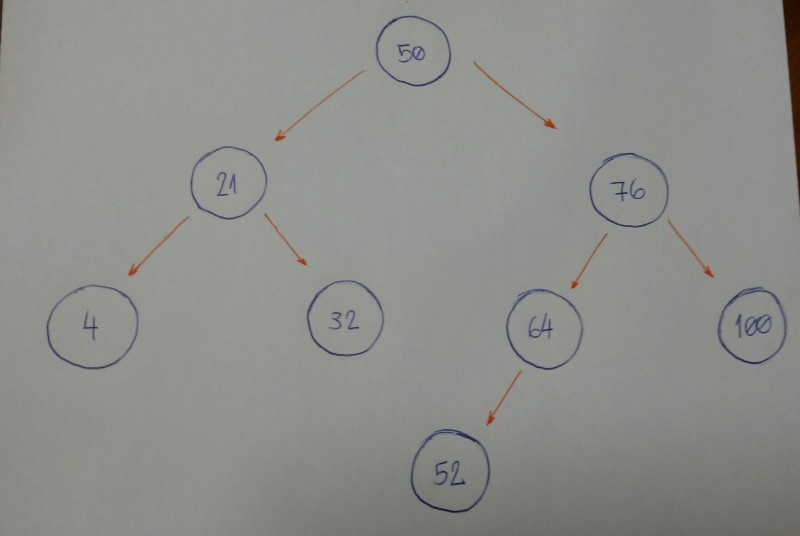
Do you notice a design here?

Permit'south pause it down.

Is the new node value greater or smaller than the current node?
If the value of the new node is greater than the electric current node, go to the right subtree. If the current node doesn't take a right child, insert it there, or else backtrack to footstep #ane.
If the value of the new node is smaller than the electric current node, get to the left subtree. If the electric current node doesn't have a left child, insert it there, or else backtrack to step #1.
We did not handle special cases hither. When the value of a new node is equal to the current value of the node, utilise dominion number 3. Consider inserting equal values to the left side of the subtree.

Now allow'due south lawmaking information technology.

                class BinarySearchTree:     def __init__(cocky, value):         self.value = value         self.left_child = None         cocky.right_child = None      def insert_node(self, value):         if value <= self.value and self.left_child:             self.left_child.insert_node(value)         elif value <= self.value:             self.left_child = BinarySearchTree(value)         elif value > self.value and self.right_child:             self.right_child.insert_node(value)         else:             self.right_child = BinarySearchTree(value)

It seems very simple.

The powerful office of this algorithm is the recursion part, which is on line 9 and line thirteen. Both lines of code call the insert_node method, and use it for its left and right children, respectively. Lines xi and 15 are the ones that practice the insertion for each child.

Let's search for the node value… Or non…

The algorithm that we will build now is well-nigh doing searches. For a given value (integer number), we will say if our Binary Search Tree does or does non accept that value.

An of import item to annotation is how we divers the tree insertion algorithm. First nosotros have our root node. All the left subtree nodes will take smaller values than the root node. And all the right subtree nodes will have values greater than the root node.

Let'due south accept a look at an case.

Imagine that we accept this tree.

Now we want to know if we have a node based on value 52.

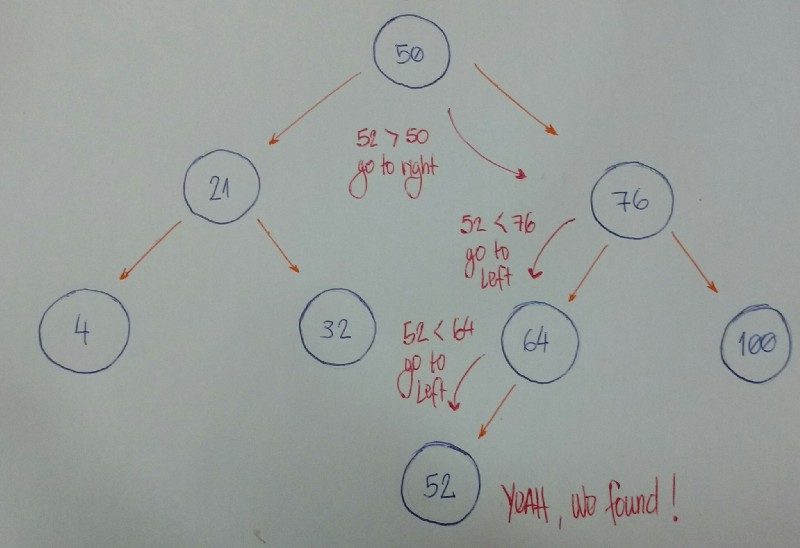
Let's break information technology downward.

We beginning with the root node as our current node. Is the given value smaller than the current node value? If yes, then nosotros will search for it on the left subtree.
Is the given value greater than the current node value? If yeah, so nosotros will search for it on the right subtree.
If rules #1 and #ii are both false, we can compare the current node value and the given value if they are equal. If the comparison returns true, then we can say, "Yes! Our tree has the given value," otherwise, we say, "Nooo, information technology hasn't."

At present let's lawmaking it.

                course BinarySearchTree:     def __init__(self, value):         cocky.value = value         cocky.left_child = None         cocky.right_child = None      def find_node(self, value):         if value < self.value and self.left_child:             return self.left_child.find_node(value)         if value > cocky.value and self.right_child:             return cocky.right_child.find_node(value)          return value == self.value

Permit's beak down the code:

Lines eight and ix fall nether rule #i.
Lines 10 and 11 fall nether rule #2.
Line xiii falls under rule #3.

How practise we test it?

Permit's create our Binary Search Tree by initializing the root node with the value fifteen.

                bst = BinarySearchTree(xv)

And at present we will insert many new nodes.

                bst.insert_node(x) bst.insert_node(8) bst.insert_node(12) bst.insert_node(xx) bst.insert_node(17) bst.insert_node(25) bst.insert_node(xix)

For each inserted node , we will examination if our find_node method really works.

                print(bst.find_node(15)) # True print(bst.find_node(ten)) # True impress(bst.find_node(8)) # Truthful print(bst.find_node(12)) # Truthful print(bst.find_node(20)) # True print(bst.find_node(17)) # True print(bst.find_node(25)) # True print(bst.find_node(xix)) # True

Yeah, it works for these given values! Let's exam for a value that doesn't exist in our Binary Search Tree.

                print(bst.find_node(0)) # Simulated

Oh yeah.

Our search is done.

Deletion: removing and organizing

Deletion is a more than complex algorithm because we need to handle different cases. For a given value, nosotros need to remove the node with this value. Imagine the following scenarios for this node : it has no children, has a single kid, or has two children.

Scenario #one: A node with no children (leaf node).

                #        |50|                              |50| #      /      \                           /    \ #    |30|     |70|   (DELETE 20) --->   |30|   |70| #   /    \                                \ # |20|   |twoscore|                             |40|

If the node we want to delete has no children, we simply delete it. The algorithm doesn't demand to reorganize the tree.

Scenario #2: A node with only one child (left or right child).

                #        |fifty|                              |fifty| #      /      \                           /    \ #    |30|     |70|   (DELETE thirty) --->   |xx|   |70| #   /             # |20|

In this case, our algorithm needs to make the parent of the node signal to the kid node. If the node is the left child, we brand the parent of the left child point to the kid. If the node is the right kid of its parent, we brand the parent of the correct child betoken to the child.

Scenario #3: A node with two children.

                #        |l|                              |50| #      /      \                           /    \ #    |xxx|     |70|   (DELETE thirty) --->   |xl|   |seventy| #   /    \                             / # |twenty|   |xl|                        |20|

When the node has 2 children, we need to discover the node with the minimum value, starting from the node'southwardright kid. We volition put this node with minimum value in the place of the node we desire to remove.

It's fourth dimension to code.

                def remove_node(self, value, parent):     if value < self.value and self.left_child:         return self.left_child.remove_node(value, self)     elif value < self.value:         render False     elif value > self.value and self.right_child:         render self.right_child.remove_node(value, self)     elif value > self.value:         return False     else:         if self.left_child is None and self.right_child is None and self == parent.left_child:             parent.left_child = None             self.clear_node()         elif self.left_child is None and self.right_child is None and self == parent.right_child:             parent.right_child = None             self.clear_node()         elif self.left_child and self.right_child is None and cocky == parent.left_child:             parent.left_child = self.left_child             self.clear_node()         elif cocky.left_child and self.right_child is None and cocky == parent.right_child:             parent.right_child = self.left_child             self.clear_node()         elif self.right_child and self.left_child is None and self == parent.left_child:             parent.left_child = cocky.right_child             self.clear_node()         elif self.right_child and self.left_child is None and self == parent.right_child:             parent.right_child = self.right_child             self.clear_node()         else:             self.value = cocky.right_child.find_minimum_value()             cocky.right_child.remove_node(self.value, self)          return True

First: Note the parameters value and parent. We want to find the nodethat has this value , and the node's parent is important to the removal of the node.
Second: Note the returning value. Our algorithm will render a boolean value. Information technology returns True if it finds the node and removes it. Otherwise it will return Faux.
From line two to line nine: Nosotros commencement searching for the node that has the valuethat nosotros are looking for. If the value is smaller than the electric current nodevalue , nosotros get to the left subtree, recursively (if, and only if, the current node has a left child). If the value is greater, go to the right subtree, recursively.
Line ten: We start to think about the remove algorithm.
From line 11 to line 13: We cover the node with no children , and information technology is the left kid from its parent. We remove the node past setting the parent'south left kid to None.
Lines xiv and xv: We cover the node with no children , and it is the right child from it's parent. We remove the node by setting the parent'south right kid to None.
Articulate node method: I will show the clear_node code below. It sets the nodes left kid , correct child, and its value to None.
From line sixteen to line 18: We cover the node with just one child (left kid), and it is the left child from it'south parent. We set the parent's left child to the node's left child (the only child it has).
From line 19 to line 21: We cover the node with just i kid (left child), and it is the right child from its parent. Nosotros gear up the parent'due south correct kid to the node's left child (the only child it has).
From line 22 to line 24: We comprehend the node with simply ane child (right child), and it is the left kid from its parent. We fix the parent'due south left child to the node's correct child (the only child information technology has).
From line 25 to line 27: We cover the node with but one kid (right child) , and it is the correct child from its parent. Nosotros set the parent's right child to the node'due south right child (the only kid it has).
From line 28 to line 30: We cover the node with both left and rightchildren. We get the node with the smallest value (the lawmaking is shown beneath) and ready information technology to the value of the current node . Stop information technology by removing the smallest node.
Line 32: If we find the node nosotros are looking for, it needs to return True. From line 11 to line 31, we handle this case. So just return Truthful and that's it.

To use the clear_node method: set up the None value to all three attributes — (value, left_child, and right_child)

                def clear_node(self):     cocky.value = None     cocky.left_child = None     cocky.right_child = None

To apply the find_minimum_value method: go way down to the left. If we tin't notice anymore nodes, we establish the smallest ane.

                def find_minimum_value(self):     if self.left_child:         render cocky.left_child.find_minimum_value()     else:         render self.value

Now allow's exam it.

We will use this tree to test our remove_node algorithm.

                #        |fifteen| #      /      \ #    |10|     |20| #   /    \    /    \ # |8|   |12| |17| |25| #              \ #              |19|

Let's remove the node with the value 8. It's a node with no child.

                print(bst.remove_node(eight, None)) # True bst.pre_order_traversal()  #     |15| #   /      \ # |10|     |20| #    \    /    \ #   |12| |17| |25| #          \ #          |nineteen|

At present let's remove the node with the value 17. It's a node with but one kid.

                print(bst.remove_node(17, None)) # Truthful bst.pre_order_traversal()  #        |15| #      /      \ #    |x|     |20| #       \    /    \ #      |12| |19| |25|

Finally, we will remove a node with 2 children. This is the root of our tree.

                impress(bst.remove_node(fifteen, None)) # True bst.pre_order_traversal()  #        |19| #      /      \ #    |10|     |20| #        \        \ #        |12|     |25|

The tests are now done. :)

That'due south all for at present!

Nosotros learned a lot here.

Congrats on finishing this dense content. It's really tough to empathize a concept that we do non know. But y'all did information technology. :)

This is i more step frontward in my journeying to learning and mastering algorithms and data structures. You tin can see the documentation of my complete journey hither on my Renaissance Developer publication.

Accept fun, keep learning and coding.

My Twitter & Github. ☺

Boosted resource

Introduction to Tree Data Construction by mycodeschool
Tree by Wikipedia
How To Not Be Stumped By Trees past the talented Vaidehi Joshi
Intro to Trees, Lecture by Professor Jonathan Cohen
Intro to Trees, Lecture by Professor David Schmidt
Intro to Trees, Lecture by Professor Victor Adamchik
Trees with Gayle Laakmann McDowell
Binary Tree Implementation and Tests by TK
Coursera Course: Information Structures by Academy of California, San Diego
Coursera Course: Data Structures and Performance by University of California, San Diego
Binary Search Tree concepts and Implementation by Paul Programming
Binary Search Tree Implementation and Tests by TK
Tree Traversal by Wikipedia
Binary Search Tree Remove Node Algorithm by GeeksforGeeks
Binary Search Tree Remove Node Algorithm by Algolist
Learning Python From Zero to Hero

Learn to lawmaking for free. freeCodeCamp's open source curriculum has helped more than 40,000 people go jobs as developers. Get started

obrienthourojece.blogspot.com

Source: https://www.freecodecamp.org/news/all-you-need-to-know-about-tree-data-structures-bceacb85490c/